ביטקוין: מערכת שיתופית לכסף אלקטרוני
נכתב על ידי Satoshi Nakamoto סאטושי נאקמוטו (satoshin@gmx.com, www.bitcoin.org).
תירגם: מני רוזנפלד
תקציר
גרסה שיתופית לחלוטין של כסף אלקטרוני תאפשר לשלוח תשלומי זמן-אמת ישירות מצד אחד לאחר מבלי לעבור דרך מוסד כספי. חתימות דיגיטליות מהוות חלק מהפתרון, אולם עיקר התועלת תאבד אם עדיין נדרש צד שלישי נאמן בכדי למנוע ניצול כפול. אנו מציעים פתרון לבעיית הניצול הכפול באמצעות רשת שיתופית. הרשת מייצרת חותמות זמן עבור תנועות על ידי גיבובן לשרשרת מתמשכת של הוכחות-עבודה מבוססות גיבוב, ובכך יוצרת תיעוד שאינו ניתן לשינוי ללא ביצוע חדש של הוכחת-העבודה. השרשרת הארוכה ביותר משמשת לא רק כהוכחה לסדר האירועים שנצפו, אלא גם הוכחה שהיא הגיעה מהריכוז הגדול ביותר של כוח חישובי. כל עוד מרבית כוח החישוב נשלט על ידי צמתים שאינם משתפים פעולה כדי לתקוף את הרשת, הם ייצרו את השרשרת הארוכה ביותר במהירות גבוהה מאשר התוקפים. הרשת עצמה דורשת מבנה מזערי. הודעות מופצות על בסיס מאמץ מיטבי, וצמתים יכולים לעזוב את הרשת ולהצטרף אליה כרצונם, ולקבל את שרשרת הוכחת-העבודה הארוכה ביותר כהוכחה על מה שקרה בהיעדרם.
1. מבוא
מסחר באינטרנט כיום מסתמך באופן כמעט בלעדי על מוסדות פיננסיים המשמשים כצד שלישי נאמן לעיבוד תשלומים אלקטרוניים. המערכת עובדת באופן משביע רצון עבור רוב העסקאות, אך עם זאת, היא עדיין סובלת מהחולשות הטבועות במודל מבוסס האמון. תנועות שהן לחלוטין בלתי ניתנות לביטול אינן באמת אפשריות, מכיוון שהמוסד הפיננסי אינו יכול להימנע מגישור מחלוקות. עלות הגישור מעלה את עלויות העסקה, מה שמגביל את הגודל המעשי המזערי לעסקה ומונע את האפשרות לעסקאות מזדמנות קטנות, ויש עלות נרחבת עוד יותר באובדן היכולת לבצע תשלומים בלתי ניתנים לביטול עבור שירותים בלתי ניתנים לביטול. האפשרות לביטול מרחיבה את הצורך באמון. סוחרים חייבים להיזהר מלקוחותיהם, ולהטריח אותם לספק יותר מידע מאשר היה נחוץ אחרת. אחוז מסוים של הונאות נתפס כבלתי נמנע. עלויות אלו וחוסר הוודאות בתשלומים היו יכולים להימנע במסחר פנים אל פנים ושימוש במטבע פיזי, אך לא קיים מנגנון המאפשר ביצוע תשלומים על גבי ערוץ תקשורת ללא צד נאמן.
נחוצה מערכת תשלומים אלקטרוניים המבוססת על הוכחה קריפטוגרפית במקום על אמון, המאפשרת לכל שני צדדים הרוצים בכך לבצע עסקה זה עם זה באופן ישיר ללא צורך בצד שלישי נאמן. עסקאות שמבחינה חישובית לא מעשי לבטל אותן יגנו על מוכרים מפני הונאה, וניתן בקלות לממש מנגנוני נאמנות (escrow) בכדי להגן על קונים. במאמר זה אנו מציעים פתרון לבעיית הניצול הכפול, על ידי שימוש בשרת חותמות-זמן חברתי ומבוזר המייצר הוכחה חישובית של הסדר הכרונולוגי של התנועות. המערכת בטוחה כל עוד הצמתים הישרים (honest) שולטים יחד ביותר עוצמת חישוב מכל קבוצת צמתים תוקפים המשתפים פעולה.
2. תנועות
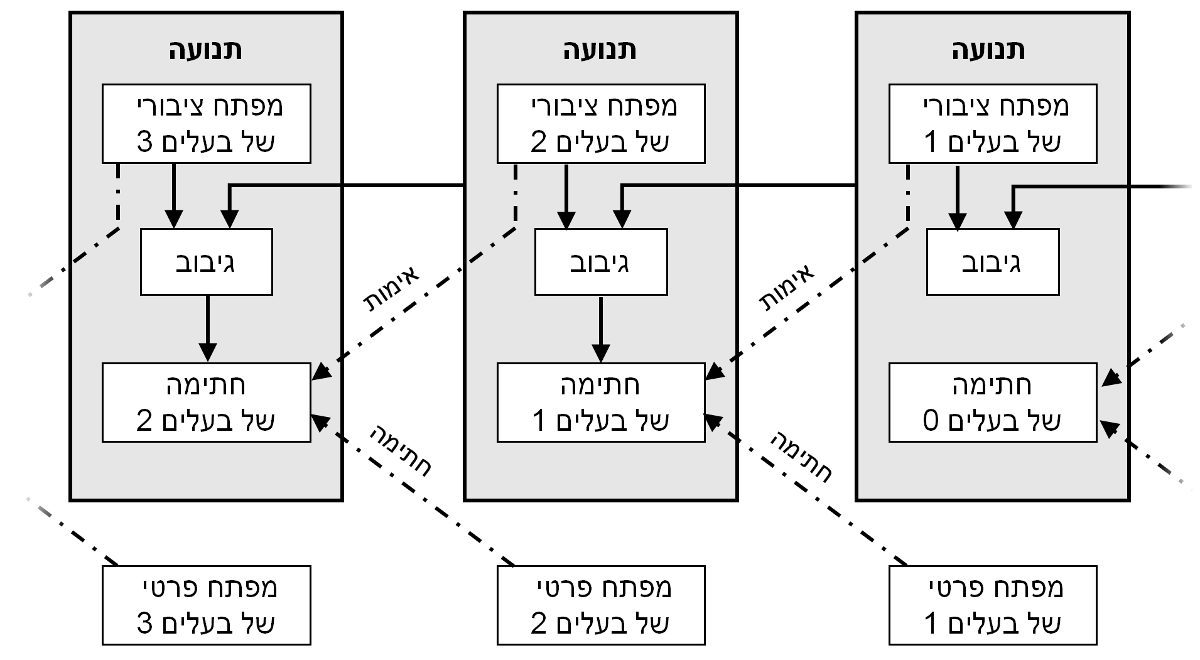
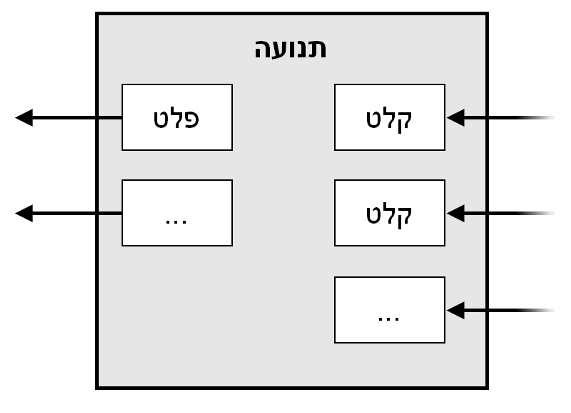
אנו מגדירים מטבע אלקטרוני כשרשרת של חתימות דיגיטליות. כל בעלים מעביר את המטבע לבא אחריו על ידי הוספת חתימת גיבוב (Hash) של התנועה (transaction) הקודמת והמפתח הציבורי של הבעלים הבאים, והוספת אלו לסוף המטבע. מקבל תשלום יכול לאמת את החתימות בכדי לוודא את שרשרת הבעלות.
הבעיה היא כמובן שמקבל התשלום אינו יכול לוודא שאף אחד מהבעלים לא ביצע ניצול כפול של המטבע (double-spend). פתרון נפוץ הוא להכניס סמכות מרכזית הזוכה לאמון, או מִטְבעה, הבודקת כל תנועה למניעת ניצול כפול. לאחר כל תנועה, המטבע חייב לחזור אל המטבעה כדי להנפיק מטבע חדש, ורק על מטבעות שהונפקו ישירות מהמטבעה סומכים שלא עברו ניצול כפול. הבעיה בפתרון זה הוא שהגורל של המערכת הכספית בכללותה תלוי בחברה המפעילה את המטבעה, היות וכל תנועה חייבת לעבור דרכה, בדיוק כמו בבנק.
אנו זקוקים לדרך בה מקבל התשלום יוכל לדעת שהבעלים הקודמים לא חתם על אף תנועה מוקדמת יותר. לצרכים שלנו, התנועה המוקדמת ביותר היא הקובעת, כך שאיננו דואגים בגין ניסיונות מאוחרים יותר לניצול כפול. הדרך היחידה לאשר את העדר תנועה היא להיות מודע לכל התנועות. במודל מבוסס מטבעה, המטבעה מודעת לכל התנועות ומחליטה איזו הגיעה קודם. כדי להשיג זאת ללא צד נאמן, חובה להכריז על התנועות באופן פומבי [1], ונחוצה מערכת להסכמה בין משתתפים לגבי היסטוריה יחידה של הסדר בו הן התקבלו. מקבל התשלום זקוק להוכחה שבזמן בו כל תנועה התבצעה, רוב הצמתים הסכימו כי היא היתה הראשונה שהתקבלה.
3. שרת חותמת-זמן
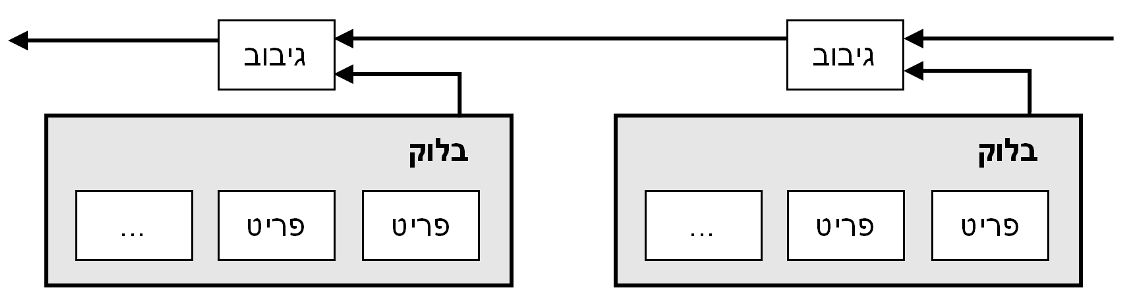
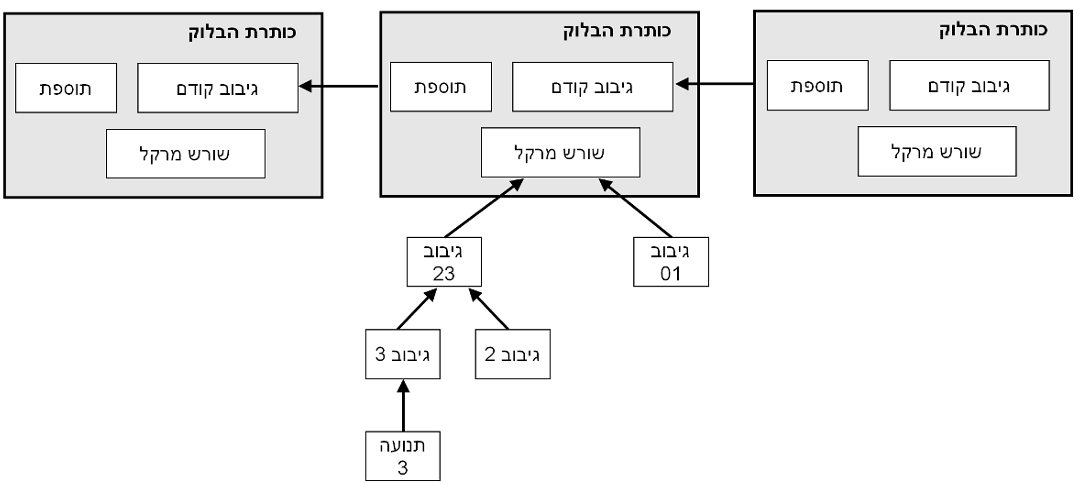
הפתרון אותו אנו מציעים מתחיל עם שרת חותמות-זמן (timestamp server). שרת חותמות-זמן פועל על ידי לקיחת גיבוב של בלוק (block) של פריטים הזקוקים לחותמת זמן והפצתו באופן נרחב, למשל בעיתון או פוסט ב-Usenet. חותמת הזמן מוכיחה שהנתונים בהכרח היו קיימים באותו זמן, כמובן, כדי להיות כלולים בגיבוב. כל חותמת-זמן מכילה את חותמת-הזמן הקודמת בגיבוב שלה, מה שיוצר שרשרת בה כל חותמת-זמן נוספת מחזקת את אלו שבאו לפניה.
4. הוכחת עבודה
בכדי לממש שרת חותמות-זמן על בסיס חברתי, אנו נצטרך מערכת הוכחת-עבודה (Proof-of-work) בדומה ל-Hashcash של אדם בק [6], במקום פרסומים בעיתון או ב-Usenet. הוכחת-העבודה כרוכה בחיפוש אחר ערך שכאשר הוא עובר גיבוב, למשל עם SHA-256, הגיבוב מתחיל במספר מסוים של סיביות אפס. כמות העבודה הנדרשת בממוצע היא מעריכית במספר סיביות האפס הנדרשות, והיא יכולה להיות מאומתת בביצוע גיבוב בודד.
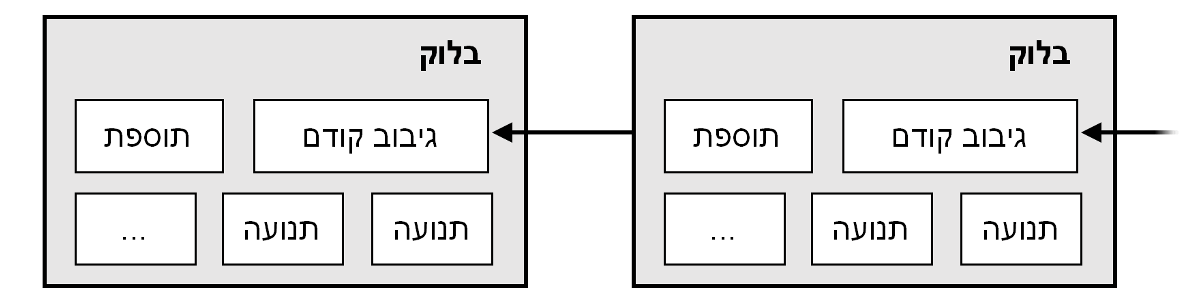
בשביל רשת חותמות-הזמן שלנו, אנו מממשים את הוכחת-העבודה על ידי הוספת מספר חד-פעמי (nonce) לבלוק עד שנמצא ערך המעניק לתוצאת גיבוב הבלוק את המספר הנדרש של סיביות אפס. לאחר שהמאמץ החישובי הושקע על מנת לגרום לבלוק לספק את הוכחת-העבודה, לא ניתן לשנות אותו מבלי לבצע את העבודה מחדש. מאחר שבלוקים מאוחרים יותר משורשרים אחריו, העבודה הדרושה כדי לשנות בלוק תכלול ביצוע מחדש של כל הבלוקים שאחריו.
הוכחת-העבודה גם פותרת את בעיית קביעת הייצוג בקבלת החלטות מבוססת רוב. אם הרוב היה מבוסס על "קול לכל כתובת IP", כל מי שמסוגל להקצות כתובות רבות היה יכול לחתור תחתיו. הוכחת עבודה היא למעשה "קול לכל מעבד (CPU)". החלטת הרוב מיוצגת על ידי השרשרת הארוכה ביותר, בה מושקע מאמץ הוכחת-העבודה הרב ביותר. אם רוב עוצמת החישוב נשלט על ידי צמתים ישרים, השרשרת הישרה תצמח בקצב המהיר ביותר ותשיג כל שרשרת מתחרה. בכדי לשנות בלוק מהעבר, תוקף יצטרך לבצע מחדש את הוכחת-העבודה של הבלוק וכל הבלוקים לאחריו, ואז להדביק את הפער ולנצח את העבודה של הצמתים הישרים. מאוחר יותר נראה שההסתברות שתוקף איטי יותר ידביק את הפער, קטנה באופן מעריכי ככל שבלוקים עוקבים מתווספים.
בכדי לפצות על הגדילה במהירות החומרה והשתנות רמת העניין בהפעלת צמתים לאורך זמן, דרגת הקושי של הוכחת-העבודה נקבעת על ידי ממוצע נע, המכוון למספר ממוצע מסוים של בלוקים לשעה. אם הבלוקים נוצרים מהר מדי, דרגת הקושי עולה.
5. רשת
השלבים בהפעלת הרשת הם כדלקמן:
צמתים תמיד מתייחסים לשרשרת הארוכה ביותר כאל השרשרת הנכונה וימשיכו לעבוד על הארכתה. אם שני צמתים משדרים גרסאות שונות של הבלוק הבא בו זמנית, חלק מהצמתים יקבלו את האחד או את השני תחילה. במקרה זה, הם יעבדו על הראשון שהם קיבלו, אבל ישמרו את הענף השני למקרה שהוא יֵהפך לארוך יותר. התיקו יישבר כשהוכחת-העבודה הבאה תימצא ואחד מהענפים יהפך לארוך יותר; הצמתים שעבדו על הענף האחר יעברו לענף הארוך יותר.
שידורים של תנועות חדשות לא צריכים בהכרח להגיע לכל הצמתים. כל עוד הם מגיעים לצמתים רבים, הם ייכנסו לתוך בלוק בחלוף זמן לא רב. שידורי בלוק גם סובלניים לגבי הודעות שנשמטו. אם צומת לא מקבל בלוק, הוא יבקש אותו לאחר שיקבל את הבלוק הבא ומשהבין שהוא החמיץ אחד.
6. תמריץ
על פי המוסכמה, הפעולה הראשונה בכל בלוק היא פעולה מיוחדת היוצרת מטבע חדש שבבעלותו של יוצר הבלוק. זה מוסיף תמריץ לצמתים לתמוך ברשת, ומעניק דרך ראשונית להפיץ מטבעות אל המחזור, מאחר שאין סמכות מרכזית המנפיקה אותם. התוספת הקבועה של מטבעות חדשים מקבילה לכורי זהב המוציאים משאבים כדי להוסיף זהב למחזור. במקרה שלנו, המשאבים הם זמן מעבד ואנרגיה חשמלית.
התמריץ יכול גם להיות ממומן על ידי עמלות פעולה. אם ערך הפלט של תנועה נמוך מערך הקלט, ההפרש הוא עמלת פעולה שמתווספת לערך התמריץ של הבלוק המכיל את התנועה. לאחר שמספר קבוע מראש של מטבעות נכנס למחזור, התמריץ יכול לעבור באופן בלעדי לעמלות פעולה ולהיות נקי לחלוטין מאינפלציה.
התמריץ יכול לעזור בעידוד צמתים להישאר ישרים. אם תוקף חמדן מסוגל לאגד יותר כוח חישוב מכל הצמתים הישרים, הוא יצטרך לבחור בין שימוש בו כדי להונות אנשים בגנבת התשלומים שלו בחזרה, או שימוש בו ליצירת מטבעות חדשים. מתקבל על הדעת שיהיה זה רווחי יותר בעיניו לשחק לפי הכללים, כללים המתגמלים אותו ביותר מטבעות חדשים לעומת כל השאר ביחד, מאשר לחתור תחת המערכת ולערער את תקפות ההון שלו עצמו.
7. שחרור נפח-כונן
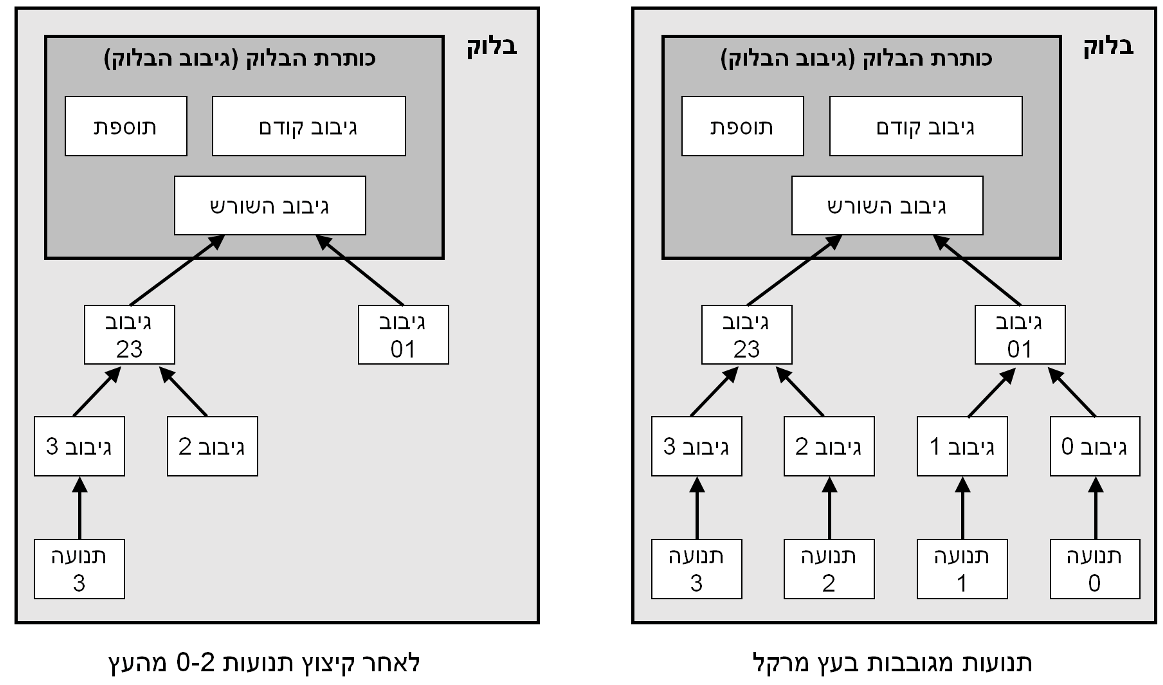
מהרגע בו התנועה האחרונה במטבע קבורה תחת מספיק בלוקים, התנועות המנוצלות לפניה יכולות להיזרק כדי לחסוך בנפח כונן. כדי לסייע בכך מבלי לשבור את גיבוב הבלוק, התנועות מגובבות בעץ מרקל (Merkle Tree), באופן שרק השורש כלול בגיבוב הבלוק. בלוקים ישנים יכולים לעבור צמצום על ידי גדימת ענפים מהעץ. אין צורך לשמור את הגיבובים הפנימיים.
כותרת בלוק (Header) ללא תנועות תהיה בערך בגודל של 80 בתים. אם אנו מניחים שבלוקים נוצרים כל 10 דקות, מדובר ב-80 בתים * 6 * 24 * 365 = 4.2MB לשנה. בהינתן שמערכות מחשב באופן טיפוסי נמכרות עם 2GB זיכרון, נכון לשנת 2008, וחוק מור צופה צמיחה עכשווית של 1.2GB לשנה, לא אמורה להיות בעיית אחסון גם אם חובה לשמור את כותרות הבלוקים בזיכרון.
8. אימות פשוט שהתבצע תשלום
ניתן לאמת תשלומים מבלי להפעיל צומת רשת מלא. משתמש צריך רק לשמור עותק של כותרות הבלוקים של שרשרת הוכחות-העבודה הארוכה ביותר, אותו הוא יכול לקבל על ידי שאילתות לצמתים ברשת עד שהוא משוכנע שיש לו את השרשרת הארוכה ביותר, ולהשיג את ענף המרקל המקשר את התנועה לבלוק בו היא חתומה בחותמת זמן. הוא לא יכול לבדוק את התנועה בעצמו, אבל על ידי קישורה למקום בשרשרת, הוא יכול לראות שצומת ברשת אישר אותה, ובלוקים שמתווספים אחריה מהווים אישוש נוסף שהרשת מסכימה איתה.
בתור שכזה, האימות הוא אמין כל עוד צמתים ישרים שולטים ברשת, אבל הוא פגיע יותר אם תוקף גובר על הרשת. בעוד צמתים ברשת יכולים לאמת תנועות בעצמם, השיטה הפשוטה יכולה ללכת שולל אחר תנועות בדיוניות של תוקף כל עוד הוא יכול להמשיך לגבור על הרשת. אסטרטגיה אחת להגן מפני זה היא לקבל התרעות מצמתים ברשת כשהם חושפים בלוק לא קביל, ולהניע את התוכנה של המשתמש להוריד את הבלוק המלא והתנועות החשודות כדי לאשר את חוסר העקביות שלהן. עסקים שמקבלים תשלומים באופן תדיר, כנראה ירצו עדיין להפעיל צמתים משל עצמם לצורך מידה רבה יותר של אבטחה בלתי תלויה ואימות מהיר יותר.
9. חלוקת ואיחוד ערך
אף על פי שהיה אפשר לטפל במטבעות באופן פרטני, יהיה זה מסורבל לבצע תנועה נפרדת לכל אגורה בהעברה. כדי לאפשר לערך להיות מחולק או לאחד מספר ערכים, תנועות מכילות מספר קלטים ופלטים. באופן רגיל יהיו או קלט אחד מתנועה קודמת גדולה יותר או קלטים מרובים המאחדים כמויות קטנות יותר, ולכל היותר שני פלטים: אחד בשביל התשלום, ואחד בשביל להחזיר את העודף, אם קיים, בחזרה אל השולח.
ראוי לציין שהסתעפות, בה כל תנועה תלויה במספר תנועות, ושתנועות אלה תלויות בעוד רבות אחרות, אינה בעיה כאן. לעולם אין צורך להפיק עותק שלם העומד בפני עצמו של היסטוריית התנועה.
10. פרטיות
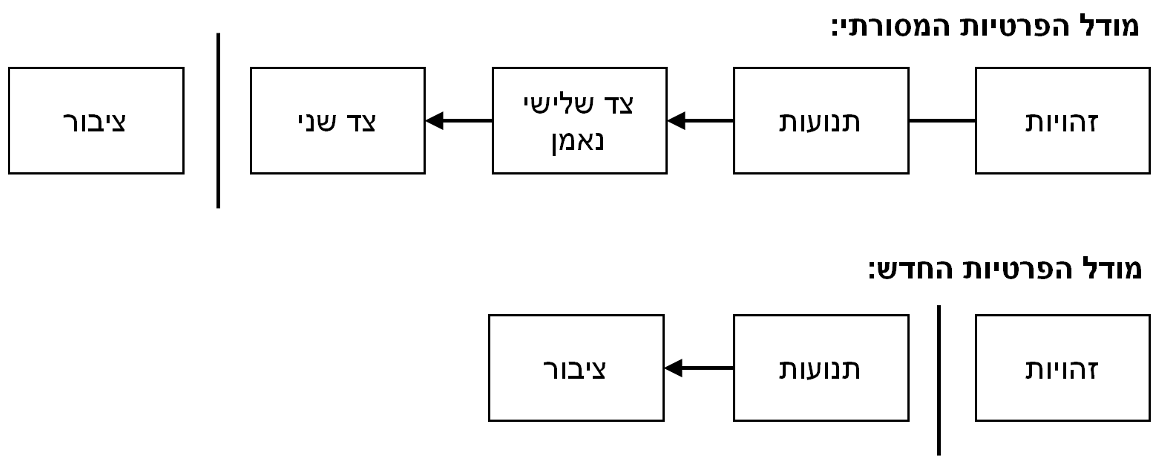
המודל הבנקאי המסורתי משיג רמה מסוימת של פרטיות בכך שהוא מגביל את הגישה למידע רק לצדדים המעורבים ולצד השלישי הנאמן. ההכרח בפרסום כל התנועות באופן פומבי מוציא מכלל חשבון את השיטה הזאת, אבל עדיין ניתן לשמור על פרטיות על ידי שבירת זרימת המידע במקום אחר - שמירת האלמוניות של המפתחות הציבוריים. הציבור יכול לראות שמישהו שולח סכום מסוים למישהו אחר, אבל ללא מידע המקשר את התנועה למישהו. זה דומה לרמת המידע המשוחרר על ידי בורסות, בהן זמן הפעולה וגודל התנועות, הרצף, מוצג באופן פומבי, אך מבלי לומר מי היו הצדדים.
כחומת אש נוספת, יש להשתמש בזוג מפתחות חדש לכל פעולה כדי למנוע מהם להיות מקושרים לבעלים משותף. מידה מסוימת של קישור היא עדיין בלתי נמנעת בתנועות מרובות קלטים, שבהכרח חושפות שהקלטים שלהן היו שייכים לאותו בעלים. הסיכון הוא שאם הבעלים של מפתח נחשף, קישור יכול לחשוף תנועות נוספות ששייכות לאותו בעלים.
11. חישובים
אנו בוחנים תרחיש בו תוקף מנסה ליצור שרשרת חלופית מהר יותר מהשרשרת הישרה. גם אם הדבר מתבצע, זה לא גורם לחשיפת המערכת לשינויים שרירותיים, כמו יצירת ערך יש מאין או לקיחת כסף שמעולם לא היה שייך לתוקף. צמתים לא יסכימו לקבל פעולה בלתי קבילה כתשלום, וצמתים ישרים לעולם לא יסכימו עם בלוק המכיל אותן. תוקף יכול רק לנסות לשנות את אחת מהתנועות שלו כדי לקחת בחזרה כסף שהוא הוציא לאחרונה.
ניתן לאפיין את המרוץ בין השרשרת הישרה ושרשרת של תוקף בתור הילוך אקראי בינומי. מאורע ההצלחה הוא שהשרשרת הישרה מתארכת בבלוק אחד, מה שמגדיל את ההובלה בשיעור 1+, ומאורע הכישלון הוא שהשרשרת של התוקף מתארכת בבלוק אחד, מה שמפחית את הפער בשיעור 1-.
ההסתברות שתוקף ידביק את הפער מגירעון נתון מקביל לבעיית מפולת המהמר (Gambler's Ruin problem). נניח כי מהמר עם אשראי בלתי מוגבל מתחיל עם גירעון ומשחק בניסיון להגיע לאיזון תוך מספר ניסיונות היכול להיות אינסופי. אנו יכולים לחשב את ההסתברות שהוא יגיע אי-פעם לאיזון, כלומר שהתוקף ידביק אי-פעם את הפער עם השרשרת הישרה, כדלקמן:
p = ההסתברות שצומת ישר ימצא את הבלוק הבא
q = ההסתברות שהתוקף ימצא את הבלוק הבא
qz = ההסתברות שהתוקף ידביק אי-פעם את הפער מפיגור של z בלוקים
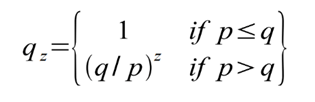
בהינתן ההנחה שלנו כי p>q, ההסתברות קטנה באופן מעריכי ככל שפער הבלוקים אותו צריך התוקף להדביק גדל. היות שהסיכויים פועלים נגדו, אם אין לו את המזל לעשות קפיצה גדולה קדימה מיד בהתחלה, הסיכויים שלו נהיים אפסיים ככל שהפיגור שלו גדל.
עתה נבחן כמה המקבל של תנועה חדשה צריך להמתין כדי להיות בטוח במידה מספיקה שהשולח אינו יכול לשנות את התנועה. אנו מניחים שהשולח הוא תוקף הרוצה לגרום למקבל להאמין לזמן-מה שהוא שילם לו, ואז להפוך את הפעולה כדי לשלם בחזרה לעצמו. המקבל יקבל התרעה כשזה יקרה, אך התוקף מקווה שזה יהיה מאוחר מדי.
המקבל יוצר זוג מפתחות חדש ונותן את המפתח הציבורי לשולח זמן קצר לפני החתימה. זה מונע מהתוקף להכין שרשרת בלוקים מבעוד מועד על ידי עבודה רצופה עליה עד שיש לו מספיק מזל כדי להוביל במידה מספקת, ואז לבצע את הפעולה באותו הרגע. ברגע בו התנועה נשלחת, השולח הלא-ישר מתחיל לעבוד בחשאי על שרשרת מקבילה המכילה גרסה חלופית של הפעולה שלו.
המקבל מחכה עד שהתנועה התווספה לבלוק ו-z בלוקים שורשרו אחריו. הוא לא יודע את מידת ההתקדמות המדויקת של התוקף, אבל בהנחה שהבלוקים הישרים לקחו פרק זמן ממוצע לכל בלוק, ההתקדמות האפשרית של התוקף היא משתנה פואסון עם תוחלת:
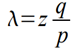
כדי למצוא את ההסתברות שהתוקף יוכל עדיין להדביק את הפער, אנו כופלים את צפיפות התפלגות פואסון לכל מידת התקדמות אפשרית בהסתברות שהוא ידביק את הפער מנקודה זו:
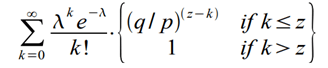
שינוי סדר האיברים כדי להימנע מסכימת הזנב האינסופי של ההתפלגות...
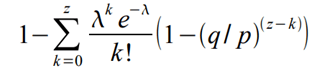
המרה לקוד בשפת C...
#include <math.h>
double AttackerSuccessProbability(double q, int z)
{
double p = 1.0 - q;
double lambda = z * (q / p);
double sum = 1.0;
int i, k;
for (k = 0; k <= z; k++)
{
double poisson = exp(-lambda);
for (i = 1; i <= k; i++)
poisson *= lambda / i;
sum -= poisson * (1 - pow(q / p, z - k));
}
return sum;
}
מהרצת מספר תוצאות, אנו יכולים לראות שההסתברות קטנה באופן מעריכי עם z.
q=0.1
z=0 P=1.0000000
z=1 P=0.2045873
z=2 P=0.0509779
z=3 P=0.0131722
z=4 P=0.0034552
z=5 P=0.0009137
z=6 P=0.0002428
z=7 P=0.0000647
z=8 P=0.0000173
z=9 P=0.0000046
z=10 P=0.0000012
q=0.3
z=0 P=1.0000000
z=5 P=0.1773523
z=10 P=0.0416605
z=15 P=0.0101008
z=20 P=0.0024804
z=25 P=0.0006132
z=30 P=0.0001522
z=35 P=0.0000379
z=40 P=0.0000095
z=45 P=0.0000024
z=50 P=0.0000006
מציאת התנאים הדרושים להסתברות קטנה מ-0.1%...
P < 0.001
q=0.10 z=5
q=0.15 z=8
q=0.20 z=11
q=0.25 z=15
q=0.30 z=24
q=0.35 z=41
q=0.40 z=89
q=0.45 z=340
12. סיכום
הצענו מערכת לתנועות אלקטרוניות שאינה מסתמכת על אמון. התחלנו עם המסגרת הרגילה של מטבעות העשויים מחתימות דיגיטליות, המספקת שליטה חזקה בבעלות, אך אינה שלמה ללא דרך למנוע ניצול כפול. כדי לפתור זאת, הצענו רשת שיתופית המשתמשת בהוכחת-עבודה כדי לנהל רישום פומבי של היסטוריית התנועות, שבמהרה הופכת לבלתי מעשית מבחינה חישובית לשינוי על ידי תוקף אם צמתים ישרים שולטים במרבית כוח החישוב. הרשת עמידה מעצם הפשטות חסרת המבנה שלה. צמתים עובדים בו זמנית עם מעט תיאום. הם אינם צריכים להזדהות, כי הודעות אינן מנותבות למקום מסוים וצריכות להימסר רק על בסיס מאמץ מיטבי. צמתים יכולים לעזוב את הרשת ולהצטרף אליה מחדש כרצונם, תוך קבלת שרשרת הוכחת-העבודה כהוכחה למה שקרה בהיעדרם. הם מצביעים עם עוצמת חישוב, ומביעים את הסכמתם עם בלוקים תקינים בעבודה על המשכתם, ודוחים בלוקים בלתי קבילים בסירוב לעבוד עליהם. כל כלל נדרש או תמריץ ניתנים לאכיפה באמצעות מנגנון קונצנזוס זה.